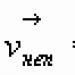Пусть дано плоское векторное поле . В дальнейшем мы будем предполагать, что функции Р и Q непрерывны вместе со своими производными и в некоторой области О плоскости
Рассмотрим в области G две произвольные точки Эти точки можно соединить различными линиями, лежащими в области вдоль которых значения криволинейного интеграла вообще говоря, различны.
Так, например, рассмотрим криволинейный интеграл
и две точки . Вычислим этот интеграл, во-первых, вдоль отрезка прямой , соединяющей точки А и В, и, во-вторых, вдоль дуги параболы соединяющей эти же точки. Применяя правила вычисления криволинейного интеграла, найдем
а) вдоль отрезка
б) вдоль дуги параболы:
Таким образом, мы видим, что значения криволинейного интеграла зависят от пути интегрирования, т. е. зависят от вида линии, соединяющей точки А и В. Наоборот, как нетрудно проверить, криволинейный интеграл вдоль тех же линий , соединяющих точки дает одно и то же значение, равное .
Разобранные примеры показывают, что криволинейные интегралы, вычисленные по различным путям, соединяющим две данные точки, в одних случаях различны между собой, а в других случаях принимают одно и то же значение.
Пусть А и В - две произвольные точки области G. Рассмотрим различные кривые, лежащие в области G и соединяющие точки А и В.
Если криволинейный интеграл по любому из этих путей принимает одно и то же значение, то говорят, что он не зависит от пути интегрирования.
В следующих двух теоремах приводятся условия, при которых криволинейный интеграл не зависит от пути интегрирования.
Теорема 1. Для того чтобы криволинейный интеграл в некоторой области G не зависел от пути интегрирования, необходимо и достаточно, чтобы интеграл по любому замкнутому контуру, лежащему в этой области, был равен нулю.
Доказательство. Достаточность.
Пусть интеграл по любому замкнутому контуру, проведенному в области G, равен нулю. Покажем, что этот интеграл не зависит от пути интегрирования. В самом деле, пусть А и В две точки, принадлежащие области G. Соединим эти точки двумя различными, произвольно выбранными кривыми лежащими в области G (рис. 257).
Покажем, что дуги образуют замкнутый контур Учитывая свойства криволинейных интегралов, получим
так как . Но по условию как интеграл по замкнутому контуру.
Следовательно, или Таким образом, криволинейный интеграл не зависит от пути интегрирования.
Необходимость. Пусть в области G криволинейный интеграл не зависит от пути интегрирования. Покажем, что интеграл по любому замкнутому контуру, лежащему в этой области, равен нулю. В самом деле, рассмотрим произвольный замкнутый контур, лежащий в области G, и возьмем на нем две произвольные точки А я В (см. рис. 257). Тогда
так как по условию . Итак, интеграл по любому замкнутому контуру L, лежащему в области G, равен нулю.
Следующая теорема дает удобные для практического использования условия, при соблюдении которых криволинейный интеграл не зависит от пути интегрирования.
Теорема 2.
Для того чтобы криволинейный интеграл не зависел от пути интегрирования в односвязной области необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие
Доказательство. Достаточность. Пусть в области Покажем, что криволинейный интеграл по любому замкнутому контуру L, лежащему в области G, равен нулю. Рассмотрим площадку а, ограниченную контуром L. В силу односвязности области G площадка а целиком принадлежит этой области. На основании формулы Остроградского-Грина частности, на площадке Поэтому а следовательно, . Итак, интеграл по любому замкнутому контуру L в области G равен нулю. На основании теоремы 1 заключаем, что криволинейный интеграл не зависит от пути интегрирования.
Необходимость. Пусть криволинейный интеграл не зависит от пути интегрирования в некоторой области Q. Покажем, что во всех точках области
Предположим противное, т. е. что в некоторой точке области Пусть для определенности . В силу предположения о непрерывности частных производных и разность будет непрерывной функцией. Следовательно, около точки можно описать круг а (лежащий в области G), во всех точках которого, как и в точке разность будет положительной. Применим к кругу формулу Остроградского-Грина.
Область называется односвязной, если ее граница представляет собой связное множество. Область называется n-связной, если ее граница распадается на n- связных множеств.
Замечание. Формула Грина верна и для многосвязных областей.
Для того, чтобы интеграл (A, B – любые точки из D) не зависел от пути интегрирования (а только от начальной и конечной точек A, B) необходимо и достаточно, чтобы по любой замкнутой кривой (по любому контуру) лежащей в D интеграл был равен нулю =0
Доказательство (необходимость). Пусть (4) не зависит от пути интегрирования. Рассмотрим произвольный контур C, лежащий в области D и выберем две произвольные точки A, B на этом контуре. Тогда кривую C можно представить, как объединение двух кривых AB=G2 , AB=G1 , C=Г - 1 + G2 .
Теорема
1. Для того, чтобы криволинейный интеграл
не зависел от пути интегрирования в D,
необходимо и достаточно чтобы
в
области D. Достаточность. Если выполнено,
то формуле Грина для любого контура C
будет
откуда по лемме следует требуемое
утверждение. Необходимость. По лемме
для любого контура= 0. Тогда по формуле Грина для области
D , ограниченной этим контуром=0. По теореме о среднем=mDили==0.
Переходя к пределу, стягивая контур к
точке, получим, что в этой точке.
Теорема 2. Для того, чтобы криволинейный интеграл (4) не зависел от пути интегрирования в D, необходимо и достаточно чтобы подинтегральное выражение Pdx+Qdy являлось полным дифференциалом некоторой функции u в области D. du = Pdx+Qdy. Достаточность. Пусть выполнено, тогда Необходимость. Пусть интеграл не зависит от пути интегрирования. Фиксируем некоторую точку A0 в области D и определим функцию u(A) = u(x,y)=
В
этом случае
XÎ (xÎ). Таким образом, существует производная =P. Аналогично, проверяется, что =Q. При сделанных предположениях функция u оказывается непрерывно - дифференцируемой и du = Pdx+Qdy.
32-33. Определение криволинейных интегралов 1 и 2 рода
Криволинейный интеграл по длине дуги (1 рода)
Пусть ф-ция f(x,y) определена и непрерывна в точках дуги АВ гладкой кривой К. Произвольно разобъем дугу на n элементарных дуг точками t0..tn пусть lk длина k частной дуги. Возьмем на каждой элементарной дуге произвольную точку N(k,k) и умножив сию точку на соотв. длину дуги составим три интегральную суммы:
1
=
f(k,k)lk
2
=
Р(k,k)хk
3
=
Q(k,k)yk,
где хk
= x k -x k -1 ,
yk
= y k -y k -1
Криволинейным
интегралом 1 рода по длине дуги будет
называться предел интегральной суммы
1
при условии, что max(lk)
0
Если
предел интегральной суммы 2
или 3
при
0, то этот предел наз. криволинейным
интегралом 2 рода, функции P(x,y)
или Q(x,y)
по кривой l
= AB
и обозначается:
или
сумму:
+
принято называть общим криволинейным
интегралом 2 рода и обозначать символом:
в этом случае ф-ции f(x,y),
P(x,y),
Q(x,y)
– называются интегрируемыми вдоль
кривой l
= AB.
Сама кривая l
наз контуром или путем интегрирования
А – начальной, В – конечной точками
интегрирования, dl
– дифференциал длины дуги, поэтому
криволинейный интеграл 1 рода наз.
криволинейным интегралом по дуге кривой,
а второго рода – по функции..
Из определения криволинейных интегралов следует, что интегралы 1 рода не зависят от того в каком направлении от А и В или от В и А пробегается кривая l. Криволинейный интеграл 1 рода по АВ:
,
для криволинейных интегралов 2 рода
изменение направления пробегания кривой
ведет к изменению знака:
В случае, когда l – замкнутая кривая т. е. т. В совпадает с т. А, то из двух возможных направлений обхода замкнутого контура l называют положительным то направление, при котором область лежащая внутри контура остается слева по отношению к??? совершающей обход, т. е. направление движения против часовой стрелки. Противоположное направление обхода наз – отрицательным. Криволинейный интеграл АВ по замкнутому контуру l пробегаемому в положит направлении будем обозначать символом:
Для пространственной кривой аналогично вводятся 1 интеграл 1 рода:
и
три интеграла 2 рода:
сумму трех последних интегралов наз. общим криволинейным интегралом 2 рода.
Некоторые приложения криволинейных интегралов 1 рода .
1.Интеграл
- длине дуги АВ
2.Механический смысл интеграла 1 рода.
Если
f(x,y)
= (x,y)
– линейная плотность материальной
дуги, то ее масса:
3.Координаты центра масс материальной дуги:
4. Момент инерции дуги лежащей в плоскости оху относительно начала координат и осей вращения ох, оу:
5. Геометрический смысл интеграла 1 рода
Пусть ф-ция z = f(x,y) – имеет размерность длины f(x,y)>=0 во всех точках материальной дуги лежащей в плоскости оху тогда:
,
где S
– площадь цилиндрической поверхности,
кот состоит из перпендикуляров плоскости
оху, вост. в точках М(x,y)
кривой АВ.
Некоторые приложения криволинейных интегралов 2 рода.
Вычисление площади плоской области D с границей L
2.Работа силы. Пусть материальная т очка под действием силы перемещается вдоль непрерывной плоской кривой ВС, направясь от В к С, работа этой силы:
Определение. Область G трехмерного пространства называется поверхностно односвяз-ной. если на любой замкнутый контур, лежащий в этой области, можно натянуть поверхность, целиком лежащую в области G. Например, внутренность сферы или все трехмерное пространство являются поверхностно односвязлыми областями; внутренность тора или трехмерное пространство, иа которого исключена прямая, поверхностно односвязными областями не являются. Пусть в поверхностно односвязной области G задан о непрерывное векторное поле Тогда имеет место следующая теорема. Теорема 9 .Для того чтобы криволинейный интеграл в поле вектора а не зависел от пути интегрирования, а зависел только от начальной и конечной точек пути (А и В), необходимо и достаточно, чтобы циркуляция вектора а вдоль любого замкнутого контура L, расположенного в области G, была равна нулю. 4 Необходимость. Пусть и т-еграл не зависит от пути интегрирования. Покажем, что тогда по любому замкнугому контуру L равен нулю. Рассмотрим произвольный замкнутый контур L в поле вектора а и возьмем на нем произвольно точки А и В (рис.35). По условию имеем - различные пути, соединяющие точни А и В\откуда как раз и есть выбранный зам!«утый контур L. Достаточность. Пусть для любого замкнутого контура L. Покажем, что в этом случае интеграл не зависит от пути интегрирования. Возьмем в поле вектора а две точки А и В, соединим их произвольными линиями L] и Ьг и покажем, что Для простоты ограничимся случаем, когда линии L\ и L2 не пересекаются. В этом случае объединение образует простой замкнутый контур L (рис. 36). По условию а по свойству аддитивности. Независимость криволинейного интеграла от пути интегрирования Потенциальное поле Вычисление криволинейного интеграла в потенциальном поле Вычисление потенциала в декартовых координатах Следовательно, откуда справедливость равенства (2) и вытекает. Теорема 9 выражает необходимое и достаточное условия независимости криволинейного интеграла от формы пути, однако эти условия трудно проверяемы. Приведем более эффективный критерий. Теорема 10. Для того, чтобы криволинейный.интеграл не зависел от пути интегрирования L, необходимо и достаточно, чтобы векторное поле было безвихревым, Здесь предполагается, что координаты) вектора а(М) имеют непрерывные частные производные первого порядка и область определения вектора а(М) поверхностно односвязна. Замечание. В силу теоремы 9 независимость криволинейного интеграла от пути интегрирования равносильна равенству нулю циркуляции век тора а вдоль любого замкнутого контура. Это обстоятельство мы используем при доказательстве теоремы. Необходимость. Пусть криволинейный интеграл не зависит от формы пути, или, что то же, циркуляция вектора а по любому замкнутому контуру L равна нулю. Тогда т. е. в каждой точке поля проекция вектора rot а на любое направление равна нулю. Это означает, что сам вектор rot а равен нулю во всех точках поля, Достаточность. Достаточность условия (3) вытекает из формулы Стокса, так как если rot а = 0, то и циркуляция вектора по любому замкнутому контуру L равна нулю: Ротор плоского поля равен что позволяет сформулировать для плоского поля следующую теорему. Теорема 11. Для того, чтобы криволинейный интеграл в односвязном плоском поле не зависел от формы линии L, необходимо и достаточно, чтобы соотношение выполнялось тождественно во всей рассматриваемой области. Если область неодносвязна, то выполнение условия вообще говоря, не обеспечивает независимости криволинейного интеграла от формы линии. Пример. Пусть Рассмотрим интеграл Ясно, что подынтегральное выражение не имеет смысла в точке 0(0,0). Поэтому исключим эту точку. В остальной части плоскости (это будет уже не односвязная область!) координаты вектора а непрерывны, имеют непрерывные частные производные и Рассмотрим интеграл (6) вдоль замкнутой кривой L - окружности радиуса R с центром в начале координат: Тогда Отличие циркуляции от нуля показывает, что интеграл (6) зависит от формы пути интегрирования. §10. Потенциальное поле Определение. Поле вектора а(М) называется потенциальным, если существует скалярная функция и(М) такая, что При этом функция и(М) называется потенциалом поля; ее поверхности уровня называются эквипотенциальными поверхностями. то соотношение (1) равносильно следующим трем скалярным равенствам: Заметим, что потенциал поля определяется с точностью до постоянного слагаемого: если следовательно, - постоянное число. Пример 1. Поле радиус-вектора г является потенциальным, так как напомним, что Потенциалом поля радиус-вектора является, следовательно. Пример 2. Поле вектора является потенциальным. Пусть функция такая, что найдена. Тогда и откуда Значит, - потенциал поля. Теорема 12. Для того чтобы паче вектора а было потенциальным, необходимо и достаточно, чтобы оно было безвихревым, т. е. чтобы его ротор равнялся нулю во всех точках поля. При этом предполагается непрерывность всех частных производных от координат вектора а и поверхностная односвязность области, в которой задан вектор а. Необходимость. Необходимость условия (2) устанавливается непосредственным подсчетом: если поле потенциально, т. е. в силу независимости смешанных производных от порядка дифференцирования. Достаточность. Пусть поле вектора безвихревое (2). Для того чтобы доказать потенциальность этого поля, построим его потенциал и(М). Из условия (2) следует, что криволинейный интеграл не зависит от формы линии L, а зависит только от ее начальной и конечной точек. Зафиксируем начальную точку а конечную точку Му, z) будем менять. Тогда интеграл (3) будет функцией точки. Обозначим эту функцию через и(М) и докажем, что В дальнейшем будем записывать интеграл (3), указывая лишь начальную и конечную точку пути интегрирования, Равенство равносильно трем скалярным равенствам Независимость криволинейного интеграла от пути интегрирования Потенциальное поле Вычисление криволинейного интеграла в потенциальном поле Вычисление потенциала в декартовых координатах Докажем первое из них, второе и третье равенст ва доказываются аналогично. По определению частной производной имеем Рассмотрим точку, близкую к точке Так как функция и(М) определяется соотношением (4), в котором криволинейный интеграл не зависит от пути интегрирования, то выберем путь интегрирования так, как указано нарис.37. Тогда Отсюда Последний интеграл берется моль отрезка прямой ММ), параллельной оси Ох. На этом отрезке в качестве параметра можно принять координату ж: Применяя к интегралу в правой части (6) теорему о среднем, получаем где величина £ заключена между. Из формулы (7) вытекает, что Так как то в силу непрерывности функции получаем Аналогично доказывается, что Следствие. Векторное поле является потенциальным тогда и только тогда, когда криво линейный интеграл в нем не зависит от пути. Вычисление криволинейного интеграла в потенциальном поле Теорема 13. Интеграл в потенциальном поле а(М) равен разности значений потенциала и(М) поля в конечной и начальной точках пути интегрирования, Ранее был о доказано, что функция является потенциалом поля. В потенциальном поле криволинейный интефал не зависит от пуги интефирования. Поэтому, выбирая путь отточки М\ к точке М2 так, чтобы он прошел через точку Afo (рис. 38), получаем или, меняя ориентацию пути в первом интефале справа, Так как потенциал поля определяется с точностью до постоянного слагаемого, то любой потенциал рассматриваемого поля можетбыть записан в виде где с - постоянная. Делая в формуле (10) замену и- с, получим для произвольного потенциала v(M) требуемую формулу Пример 3. В примере 1 было показано, что потенциалом поля радиус-вектора г является функция где - расстояние от точки до начала координат. Вычисление потенциала в декартовых координатах Пусть задано потенциальное поле Ранее было показано, что потенциальная функция «(М) может быть найдена по формуле Интеграл (11) удобнее всего вычислять так: зафиксируем начальную точку и соединим ее с достаточно близкой текущей точкой М(х, y,z) ломаной, звенья которой параллельны координатным осям, . При этом на каждом звене ломаной изменяется только одна координата, что позволяет существенно упростить вычисления. В самом деле, на отрезке М0М\ имеем: На отрезке. Рис. 39 . На отрезке. Следовательно, потенциал равен где - координаты текущей точки на звеньях ломаной, вдоль которых ведется интегрирование. Пример 4. Доказать, что векторное поле к является потенциальным, и найти его потенциал. 4 Проверим, будет ли поле вектора a(Af) потенциально. С этой це/ью вычислим ротор поля. Имеем Поле является потенциальным. Потенциал этого поля найдем с помощью формулы (12). Возьмем за начальную точку Л/о начало координат О (так обычно поступают, если поле а(М) определено в начале координат). Тогда получим Итак, где с - произвольная постоянная. Потенциал этого поля можно найти и по-иному. По определению потенциал и(х, у, z) есть скалярная функция, для которой gradu = а. Это векторное равенство равносильно трем скалярным равенствам: Интегрируя (13) по х, получим где - произвольная дифференцируемая функция ог у и г. Продифференцируем по у: Независимость криволинейного интеграла от пути интегрирования Потенциальное поле Вычисление криволинейного интеграла в потенциальном поле Вычисление потенциала в декартовых координатах Проинтегрировав (17) по у, найдем - некоторая функция z. Подставив (18) в (16), получим. Дифференцируя последнее равенство no z и учитывая соотношение (15), получим уравнение для откуда
2-го рода от пути интегрирования
Рассмотрим криволинейный интеграл 2-го рода, где L - кривая, соединяющая точки M и N. Пусть функции P(x, y) и Q(x, y) имеют непрерывные частные производные в некоторой области D, в которой целиком лежит кривая L. Определим условия, при которых рассматриваемый криволинейный интеграл зависит не от формы кривой L, а только от расположения точек M и N.
Проведем две произвольные кривые MSN и MTN, лежащие в области D и соединяющие точки M и N (рис.14).
Предположим, что, то есть
где L - замкнутый контур, составленный из кривых MSN и NTM (следовательно, его можно считать произвольным). Таким образом, условие независимости криволинейного интеграла 2-го рода от пути интегрирования равносильно условию, что такой интеграл по любому замкнутому контуру равен нулю.
Теорема 5 (теорема Грина). Пусть во всех точках некоторой области D непрерывны функции P(x, y) и Q(x, y) и их частные производные и. Тогда для того, чтобы для любого замкнутого контура L, лежащего в области D, выполнялось условие
необходимо и достаточно, чтобы = во всех точках области D.
Доказательство.
1) Достаточность: пусть условие = выполнено. Рассмотрим произвольный замкнутый контур L в области D, ограничивающий область S, и напишем для него формулу Грина:
Итак, достаточность доказана.
2) Необходимость: предположим, что условие выполнено в каждой точке области D, но найдется хотя бы одна точка этой области, в которой - ? 0. Пусть, например, в точке P(x0, y0) имеем: - > 0. Так как в левой части неравенства стоит непрерывная функция, она будет положительна и больше некоторого? > 0 в некоторой малой области D`, содержащей точку Р. Следовательно,
Отсюда по формуле Грина получаем, что
где L` - контур, ограничивающий область D`. Этот результат противоречит условию. Следовательно, = во всех точках области D, что и требовалось доказать.
Замечание 1. Аналогичным образом для трехмерного пространства можно доказать, что необходимыми и достаточными условиями независимости криволинейного интеграла
от пути интегрирования являются:
Замечание 2. При выполнении условий (52) выражение Pdx + Qdy +Rdz является полным дифференциалом некоторой функции и. Это позволяет свести вычисление криволинейного интеграла к определению разности значений и в конечной и начальной точках контура интегрирования, так как
При этом функцию и можно найти по формуле
где (x0, y0, z0) - точка из области D, a C - произвольная постоянная. Действительно, легко убедиться, что частные производные функции и, заданной формулой (53), равны P, Q и R.
Пример 10.
Вычислить криволинейный интеграл 2-го рода
по произвольной кривой, соединяющей точки (1, 1, 1) и (2, 3, 4).
Убедимся, что выполнены условия (52):
Следовательно, функция и существует. Найдем ее по формуле (53), положив x0 = y0 = z0 = 0. Тогда
Таким образом, функция и определяется с точностью до произвольного постоянного слагаемого. Примем С = 0, тогда u = xyz. Следовательно,
Рассмотрим криволинейный интеграл
взятый по некоторой плоской кривой L, соединяющей точки М и N. Будем предполагать, что функции имеют непрерывные частные производные в рассматриваемой области D. Выясним, при каких условиях написанный криволинейный интеграл не зависит от формы кривой L, а зависит только от положения начальной и конечной точек М и N.
Рассмотрим две произвольные кривые MPN и MQN, лежащие в рассматриваемой области D и соединяющие точки М и N (рис. 351). Пусть
Тогда на основании свойств 1 и 2 криволинейных интегралов (§ 1) имеем
т. e. криволинейный интеграл по замкнутому контуру
В последней формуле криволинейный интеграл взят по замкнутому контуру L, составленному из кривых . Этот контур L можно, очевидно, считать произвольным.
Таким образом, из условия, что для любых двух точек М и N криволинейный интеграл не зависит формы соединяющей их кривой, а зависит только от положения этих точек, следует, что криволинейный интеграл по любому замкнутому контуру равен нулю.
Справедливо и обратное заключение: если криволинейный интеграл по любому замкнутому контуру равен нулю, то этот криволинейный интеграл не зависит от формы кривой, соединяющей две любые точки, а зависит только от положения этих точек. Действительно, из равенства (2) следует равенство (1).
В примере 4 § 2 криволинейный интеграл не зависит от пути интегрирования, в примере 3 криволинейный интеграл зависит от пути интегрирования, так как в этом примере интеграл по замкнутому контуру не равняется нулю, а дает площадь, ограниченную рассматриваемым контуром; в примерах 1 и 2 криволинейные интегралы также зависят от пути интегрирования.
Естественно возникает вопрос: каким условиям должны удовлетворять функции для того, чтобы криволинейный интеграл по любому замкнутому контуру был равен нулю. Ответ на этот вопрос дает следующая теорема:
Теорема. Пусть во всех точках некоторой области D функции вместе со своими частными производными и непрерывны. Тогда, для того чтобы криволинейный интеграл по любому замкнутому контуру L, лежащему в области D, был равен нулю, т. е. чтобы
необходимо и достаточно выполнение равенства
во всех течках области
Доказательство. Рассмотрим произвольный замкнутый контур L в области D и для него напишем формулу Грина:
Если выполняется условие (3), то двойной интеграл, стоящий слева, тождественно равен нулю и, следовательно,
Таким образом, достаточность условия (3) доказана.
Докажем теперь необходимость этого условия, т. е. докажем, что если равенство (2) выполняется для любой замкнутой кривой L в области D, та в каждой точке этой области выполняется и условие (3).
Допустим, напротив, что равенство (2) выполняется, т. е.
а условие (3) не выполняется, т. е.
хотя бы в одной точке. Пусть, например, в некоторой точке имеем неравенство
Так как в левой части неравенства стоит непрерывная функция, то она будет положительна и больше некоторого числа во всех точках некоторой достаточно малой области D, содержащей точку . Возьмем двойной интеграл по этой области от разности . Он будет иметь положительное значение. Действительно,
Но по формуле Грина левая часть последнего неравенства равна криволинейному интегралу по границе области который равен нулю. Следовательно, последнее неравенство противоречит условию (2) и, значит, предположение, что отлично от нуля хотя бы в одной точке, неверно. Отсюда
вытекает, что
во всех точках данной области
Таким образом, теорема полностью доказана.
В § 9 гл. XIII было доказано, что выполнение условия равносильно тому, что выражение есть полный дифференциал некоторой функции , т. е.
Но в этом случае вектор
есть градиент функции функция градиент которой равен вектору называется потенциалом этого вектора. Докажем, что в этом случае криволинейный интеграл
По любой кривой L, соединяющей точки М и N, (М) равняется разности значений функции и в этих точках:
Доказательство. Если является полным дифференциалом функции то и криволинейный интеграл примет вид
Для вычисления этого интеграла напишем параметрические уравнения кривой L, соединяющей точки М и
интеграл, сведется к следующему определенному интегралу:
Выражение, стоящее в скобках, есть функция от являющаяся полной производной от функции Поэтому
Как мы видим, криволинейный интеграл от полного дифференциала не зависит от формы кривой, по которой производится интегрирование.
Аналогичное утверждение имеет место и для криволинейного интеграла по пространственной кривой (см. ниже § 7).
Замечание. Иногда приходится рассматривать криволинейные интегралы по длине дуги L от некоторой функции
